Question

A company manufactures cell phones. In August, a random sample of 125 cell phones was inspected, and 3 phones were found to be defective. The company manufactured 8,000 cell phones in August. Based on the results from the sample, about how many cell phones are expected to be defective?

Answer 1

192

Explanation:

Answer 2

192

Explanation:

To find how many phones are expected to be defective, we need to represent the values in a fraction.

`(x)/(8000)=(3)/(125)`

x = number of defective phones

Now we can solve this using algebra.

To get the value of x we need to multiply both sides by 8000 to leave x alone.

`x=(3)/(125)(8000)`

`x=0.024(8000)`

`x=192`

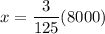
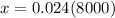
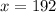
So around 192 cell phones are expected to be defective out of 8000 phones.