Answer:
Option A is correct
Common ratio = 4
Explanation:
Common ratio(r) : In a geometric series, the common ratio is the ratio of a term to the previous term.
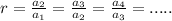
As per the statement:
The values in the table represent a exponential function.
Since, Geometric sequences and exponential functions are very closely related to each other.
At x= 1;
y = 9
At x = 2;
y = 36 and so on....
By definition we have;
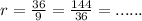
After solving we get;
r =4
Therefore, the common ratio of the associated geometric is, 4