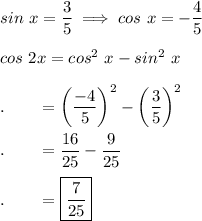You need the Unit Circle to answer these questions! (attached)
7. Answer:
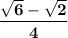
Explanation:
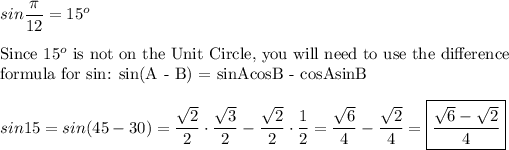
8. Answer: 0
Explanation:
The sum formula for cos is: cos (A + B) = cosA cosB - sinA sinB
Since we are given cos75° cos15° - sin75° sin15°, we can conclude that we are looking for cos (75° + 15°) = cos 90°.
The Unit Circle shows us that cos 90° = 0
9. Answer:
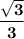
Explanation:
The given expression is for tan (A + B).
tan (10° + 20°) = tan 30° =
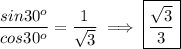
10. Answer:
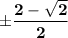
Explanation:
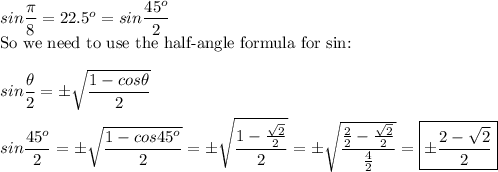
11. TOO BLURRY TO SEE THE PROBLEM
12. Answer:
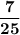
Explanation:
Quadrant II means that sin is positive and cos is negative.