Question

You and another person are sunbathing on the beach near a lifeguard station. The other person chooses a spot that is the same distance from the shoreline but 11 feet closer to the station than you. The angles of elevation from you and the other person to the top of the lifeguard station are 36 degrees and 46 degrees, respectively. Estimate the height of the lifeguard station to the nearest tenth of a foot.

Answer 1

Answer: 26.8 feet

Explanation:

In the figure attached you can see two right triangles triangle ABD and a triangle ACD.

You are located at point B and the other person at point C.

The approximate height of the lifeguard station is x.

Keep on mind that:

`tan\alpha=(opposite)/(adjacent)`

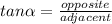
Therefore:

For the triangle ABD:

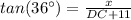`tan(36\°)=(x)/(DC+11)` [EQUATION 1]

For the triangle ACD:

`tan(46\°)=(x)/(DC)` [EQUATION 2]

Solve from DC from [EQUATION 2]:

`DC=(x)/(tan(46\°))`

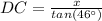
Substitute into [EQUATION 1] and solve for x:

`tan(36\°)=(x)/(((x)/(tan(46\°))+11))\\tan(36\°)((x)/(tan(46\°))+11)=x\\11*tan(36\°)=x-(xtan(36\°))/(tan(46\°))\\7.991=0.298x`

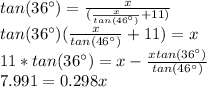
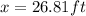`x=26.81ft`≈26.8ft