Answer: 26.8 feet
Explanation:
In the figure attached you can see two right triangles triangle ABD and a triangle ACD.
You are located at point B and the other person at point C.
The approximate height of the lifeguard station is x.
Keep on mind that:
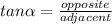
Therefore:
For the triangle ABD:
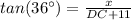 [EQUATION 1]
[EQUATION 1]
For the triangle ACD:
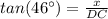 [EQUATION 2]
[EQUATION 2]
Solve from DC from [EQUATION 2]:
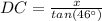
Substitute into [EQUATION 1] and solve for x:
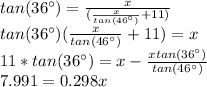
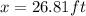 ≈26.8ft
≈26.8ft