Answer: Last option.
Explanation:
To find the inverse of the function f(x), you must follow the proccedure shown below:
- Rewrite the function,as following:
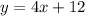
- Solve for x. Then:
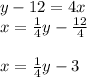
- Now, substitute y with x.
Therefore, you obtain that the inverse function g(x) is the following:
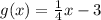
Then, the answer is the last option.