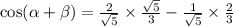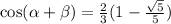Answer:
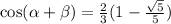
Explanation:
Let the hypotenuse of the smaller triangle be h units.
Then; from the Pythagoras Theorem.
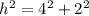
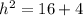
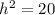
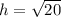
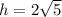
From the smaller triangle;
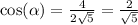 and
and
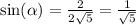
From the second triangle, let the other other shorter leg of the second triangle be s units.
Then;
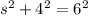
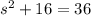
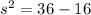
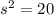
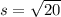
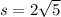
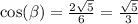
and
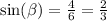
We now use the double angle property;
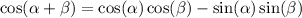
we plug in the values to obtain;