1. Find the missing side length. Round your answer to the nearest tenth. 6.7 21.3 5.5 43.2 2. Find the length of side a. Round to the nearest tenth. 12 378.4 18.3 19.5 3. Find t…

Question

asked May 7, 2020 155k views

1 Answer

Donturner · Answer 1 · 2020-05-12T08:45:39+0000

QUESTION 1

We can use the cosine rule to find the missing side length.

Recall that the cosine rule for a triangle with sides a,b,c and an included angle A is

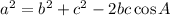
$a^2=b^2+c^2-2bc\cos A$

Let the missing side length in the triangle with sides 6, 9 and the included angle of
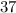$37\degree$ be
units.

We then substitute the values into the cosine rule to obtain;

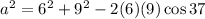
$a^2=6^2+9^2-2(6)(9)\cos 37\degree$

$a^2=36+81-108\cos 37\degree$

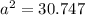
a^2=30.747

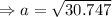
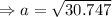
$\Rightarrow a=√(30.747)$

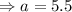$\Rightarrow a=5.5$ units to the nearest tenth.

QUESTION 2

We again use the cosine rule:
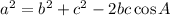
$a^2=b^2+c^2-2bc\cos A$

We substitute the given values to obtain;

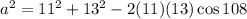
$a^2=11^2+13^2-2(11)(13)\cos 108\degree$

$a^2=121+169-286\cos 108\degree$

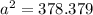
a^2=378.379

$\Rightarrow a=√(378.379)$

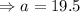$\Rightarrow a=19.5$ to the nearest tenth

QUESTION 3

We again use the cosine rule :

$|BA|^2=((1)/(2))^2+((1)/(3))^2-2((1)/(2))((1)/(3))\cos 100\degree$

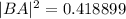
|BA|^2=0.418899

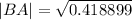
|BA|=√(0.418899)

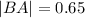|BA|=0.65 to the nearest hundredth