Answer: The force becomes four times as much
The electric force is a force that is inversely proportional to the square of the distance. This can be proved by Coulomb's Law, which states:
"The electrostatic force
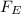 between two point charges
between two point charges
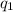 and
and
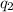 is proportional to the product of the charges and inversely proportional to the square of the distance
is proportional to the product of the charges and inversely proportional to the square of the distance
 that separates them, and has the direction of the line that joins them"
that separates them, and has the direction of the line that joins them"
Mathematically this law is written as:
 (1)
(1)
Where
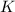 is a proportionality constant.
is a proportionality constant.
Now, if we say
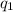 is the proton and
is the proton and
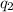 is the electron, and cut the distance between them in half, the new distance will be
is the electron, and cut the distance between them in half, the new distance will be
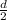 .
.
Substituting this new distance in equation (1):
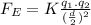 (2)
(2)
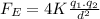 (3)>>>As we can see, the force becomes four times stronger
(3)>>>As we can see, the force becomes four times stronger