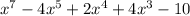Answer:
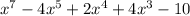
Explanation:
To write a polynomial in descending order means writing the polynomial in decreasing powers of x.
The given polynomial expresion is
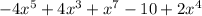
We start from the term with the highest degree and end with term with the least degree.
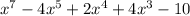
Therefore the given polynomial written in descending order is