Answer:
The function
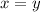 and
and
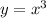 are inverse function.
are inverse function.
Explanation:
Function inverse definition:
If a provided function f(x) is mapped x to y, then the inverse of the provided function f(x) is mapped y to x.
Or
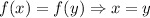
Now, consider the function y = x.
Interchange the variables x and y.
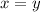
Now, solve
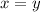 for
for
 .
.
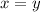
Therefore, this function has an inverse.
Consider the function
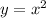 .
.
Interchange the variables x and y.
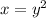
Now, solve
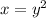 for
for
 .
.

Therefore, the function has no inverse.
Consider the function
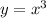 .
.
Interchange the variables x and y.
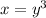
Now, solve
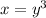 for
for
 .
.
![\sqrt[3]{x}=y](https://img.qammunity.org/2020/formulas/mathematics/middle-school/e3fq04y61gsh6qo2mxvs4oh04gervvel21.png)
Therefore, the function has inverse.
Consider the function
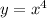 .
.
Interchange the variables x and y.
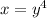
Now, solve
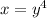 for
for
 .
.
![\pm \sqrt[4]{x}=y](https://img.qammunity.org/2020/formulas/mathematics/middle-school/c9aid8kdy1ebok0jvim6y7widmlo40nqw9.png)
Therefore, the function has no inverse.
Hence, the function
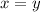 and
and
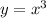 are inverse function.
are inverse function.