Question

Solve the equation. Round to the nearest hundredth. Show work.


`6e^(2x) - 13e^(x) = 5`

Answer 1

x = 0.0116096 , 1.91705119

Explanation:

I looked on a site to look this up.

Answer 2

x = 0.92

Explanation:

To solve this, we need first use the exponent rule of
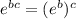`e^(bc)=(e^b)^c` on
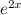`e^(2x)`. We can break it down to
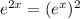`e^(2x)=(e^x)^2`. We can now re-write as:

`6(e^x)^(2)-13(e^x)-5=0`

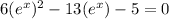
This looks like a trinomial that we can middle term factorize by letting
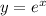`y=e^x`. Thus we can write and factorize and solve as shown below:

`6(e^x)^(2)-13(e^x)-5=0\\6y^2-13y-5=0\\6y^2+2y-15y-5=0\\2y(3y+1)-5(3y+1)=0\\(2y-5)(3y+1)=0`

Thus, 2y-5 = 0 OR 3y+1 = 0

Solving we have y = 5/2 and y = -1/3

Now bringing back the original variable of letting y = e^x, we have:

1. 5/2 = e^x, and

2. -1/3 = e^x

Solving 1:

`(5)/(2)=e^x\\ln((5)/(2))=ln(e^x)\\x=ln((5)/(2))`

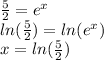
Solving 2:

We will have x = ln (-1/3) WHICH IS NOT POSSIBLE because ln is never negative.

So our answer is x = ln (5/2)

Rounding to nearest hundredth: x = 0.92