Question

Solve the equation. Round to the nearest hundredth. Show work.


`2e^(8x) = 1 - e^(4x)`

Answer 1

The value of x = -0.17

Explanation:

∵
`2e^(8x)=1-e^(4x)`

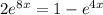
Let
`e^(4x)=y`

∴
`e^(8x)=y^(2)`

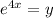
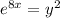
∴ 2y² = 1 - y

∴ 2y² + y - 1 =0 ⇒ factorize

∴ (2y - 1)(y + 1) = 0

∴ 2y - 1 = 0 ⇒ 2y = 1 ⇒ y = 1/2

∴ y + 1 = 0 ⇒ y = -1

∵
`y=e^(4x)`

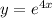
Note:
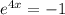`e^(4x)=-1` ⇒ refused

(
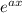`e^(ax)` never gives -ve values)

∴
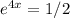`e^(4x)= 1/2` ⇒ insert ln in both sides

∵
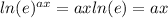`ln(e)^(ax)=axln(e)=ax` ⇒ ln(e) = 1

∴ 4xln(e) = ln(1/2) ⇒ 4x = ln(1/2)

∴ x = [ln(1/2)]/4 = -0.17