Question

A family on a vacation drives 123 miles in 2 hours then gets stuck in traffic and goes 4 miles in the next 15 minutes. The remaining 191 miles of the trip take 3 3/4 hours. What was their average rate of speed to the nearest tenth of a mile per hour

Answer 1

13

Explanation:

Answer 2

Their average rate of speed is 53 miles per hour.

Explanation:

Given : A family on a vacation drives 123 miles in 2 hours then gets stuck in traffic and goes 4 miles in the next 15 minutes. The remaining 191 miles of the trip take
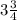`3(3)/(4)` hours.

To find : What was their average rate of speed to the nearest tenth of a mile per hour ?

Solution :

We know,
`\text{Speed}=\frac{\text{Distance}}{\text{Time}}`

Total distance traveled by family on vacation is

D= 123 miles + 4 miles + 191 miles = 318 miles

Total time taken by family on vacation is

T= 2 hours + 15 minutes +
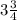`3(3)/(4)` hours

T= 2 hours +
`(15)/(60)` hours +
`3(3)/(4)` hours

T=
`2+ (1)/(4)+ (15)/(4)` hours

T=
`(8+1+15)/(4)` hours

T=
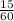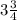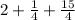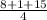`(24)/(4)` hours

T= 6 hours

Substitute the value in the formula,

`\text{Speed}=(318)/(6)`

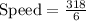
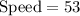`\text{Speed}=53` miles per hour.

Therefore, Their average rate of speed is 53 miles per hour.