Answer:
The point through which the circle passes is:
(2,8)
Explanation:
The equation of the circle is given by:
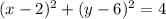
We will check by putting each point in the equation and check which is equal to 4.
1)
(2,8)
when x=2 and y=8 we have:

Hence, the circle passes through the point (2,8).
2)
(5,6)
when x=5 and y=6 we have:
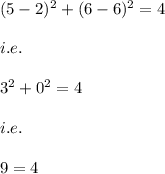
which is not true.
Hence, the circle does not pass through (5,6).
3)
(-5,6)
when x= -5 and y=6 we have:
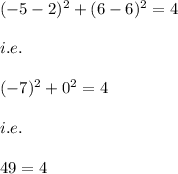
which is not true.
Hence, the circle does not pass through (-5,6).
4)
(2,-8)
when x=2 and y= -8 we have:
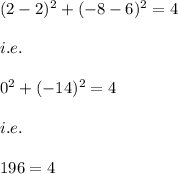
Hence, the circle does not passes through the point (2,-8).