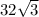Question

Find the area of the trapezoid. leave your answer in simplest radical form.

Answer 1

4th option is correct

Explanation:

Here in the triangle we have angle = 60

hypotenuse= 8

opposite and adjacent can be solved using trigonometric ratios

cos 60 =
`(adjacent)/(hupotenuse) \\(adjacent)/(8) \\(1)/(2)=(adjacent)/(8)`

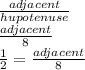
which gives adjacent = 4 on solving

likewise using sine we can find opposite side to the angle which is height of

trapezium.

sin60
`(opposite)/(hypotenuse)=(x)/(8) \\(√(3) )/(2)=(x)/(8)\\x=4√(3)`

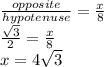
therefore height =
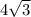`4√(3)` and adjacent = 4 ft

therefore opposite sides of Trapezium are 10 ft and 6 ft

Formula for area of Trapezium =
`(1)/(2)`(sum of parallel sides)x height

=
`(1)/(2)`(10+6)x
`4√(3)`

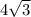
on solving it ,we get
`32√(3)`

Answer 2

= 32√3 ft²

Explanation:

Area of the trapezoid will be equal to the area of the square and that of the triangle.

Considering the triangle part;

Cos 60 = x/8

x = 8 × sin 60

= 4

Base of the triangle part = 4 ft

Therefore, top of the trapezoid = 6 ft

Height = 8 × sin 60

= 8 × √3/2

= 4 √3

Area of the trapezoid

Area = ((a+b)/2) × h

= ((6 + 10 )/2 )× 4√3

= 16/2 × 4√3

= 32√3 ft²