Answer:
center:(4,-2)
Radius: 3 units
Explanation:
The standard equation of a circle is given as
 , where (h,k) is the center and r is the radius of the circle.
, where (h,k) is the center and r is the radius of the circle.
The given equation is
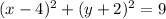 .
.
We compare to the standard equation of the circle to get;
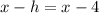
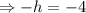
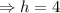
and
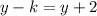
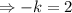
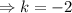
Hence the center of the circle is (4,-2).
Also, we have
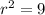
Therefore
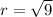
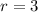 units.
units.