Question

Evaluate the log without a calculator ( Show your work )

Look at image. That is the problem.

Answer 1

8

Explanation:

Given in the question a logarithm expression

`125^(log_(5)2)`

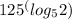
We will use Exponent of Log Rule

`b^(log_(b)k) = k`

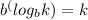
here b = 5

k = 2

Suppose

`125^(log_(5)2) = x`

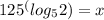
take cube root on both sides of this equation

`\sqrt[ 3]{(125^(log_(5)2)}=\sqrt[3]{x}`

`\sqrt[3]{(125)} ^(log_(5)2)=\sqrt[3]{x}`

`5^(log_(5)2)}=\sqrt[3]{x}`

Now according to the rule

2 = ∛x

to remove cube root take cube on both side

x = 8

so
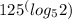`125^(log_(5)2 )` = 8