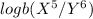Question

Condense the following logs into a single log:


`5log_(b) x - 6log_(b) y`

Answer 1

`5\log_b(x)-6\log_b(y)=\log_b((x^5)/(y^6))`

Explanation:

The given logarithmic expression is
`5\log_b(x)-6\log_b(y)`

We apply the rule:
`n\log_b(M)=\log_b(M^n)`

This implies that;

`5\log_b(x)-6\log_b(y)=\log_b(x^5)-\log_b(y^6)`

We now apply the rule;
`\log_a(M)-\log_a(N)=\log_a((M)/(N) )`

`5\log_b(x)-6\log_b(y)=\log_b((x^5)/(y^6))`

Answer 2

`logb(X^5 / Y^6)`

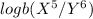
Explanation:

Given in the question an expression

5logbX - 6logbY

To Condense the following logs into a single log we will use logarithm rules

1) log power rule

5logbX = logbX^5

6logbY = logbY^6

2)log qoutient rule

ln(x/y) = ln(x)−ln(y)

logbX^5 - logbY^6 =
`logb(X^5 / Y^6)`