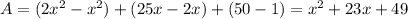Answer:
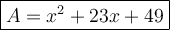
Explanation:
Subtract the area of a square (x + 1) × (x + 1)
from the area of a rectangle (x + 10) × (2x + 5)
The area of a square:
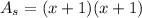 use FOIL: (a + b)(c + d) = ac + ad + bc + bd
use FOIL: (a + b)(c + d) = ac + ad + bc + bd
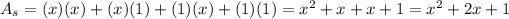
The area of a rectangle:
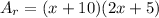 use FOIL
use FOIL
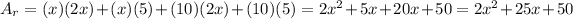
The area of a figure:
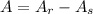
Substitute:
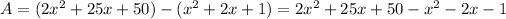
combine like terms