Answer:
The area of the octagon is
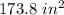
Explanation:
we know that
The area of a regular octagon is equal to the area of eight isosceles triangle
The base of each isosceles triangle is equal to the length side of the regular octagon
The vertex angle of each isosceles triangle is equal to
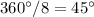
The area of each isosceles triangle is equal to

where
b is the length side of the regular octagon
h is the height of each isosceles triangle
Find the length side of the regular octagon b
The perimeter of a octagon is equal to
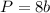

so
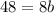
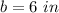
Find the height of each isosceles triangle h
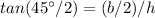

substitute the values

Find the area of the octagon
![A=8[(1)/(2)bh]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/o5rrud2lwhv5o7burhtcr8046g7nwpxuo7.png)
![A=8[(1)/(2)(6)(7.24)]=173.8\ in^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/d2f50eurfahzmk55os0upru3aj1bjvtki3.png)