Question

Can you also explain how you got the answers to this

Answer 1

Hope this helps :)

Okay so first just keep in mind the trig formulas

Sintheta= perpendicular/hypotenuse

Costheta=base/hypotenuse

Tantheta= perpendicular/base

Just remember it by " some people have curly brown hair through proper brushing"

And the Pythagorean Theorem

Perpendicular^2+Base^2=Hypotenuse^2

Okay so now our base length is x and perpendicular length is y and hypotenuse is
`√(x^2+y^2)`

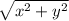
for the first three just add the information above in the answer

a)
`\frac{y}{\sqrt{x^(2)+y^(2)}}`

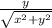
b)
`(x)/(√(x^2+y^2))`

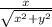
c)
`(y)/(x)`

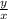
For the last three, I personally havent done them properly yet but you just reverse the formula if that makes sense

Csctheta=hypotenuse/perpendicular

Sectheta=hypotenuse/base

Cottheta=base/perpendicular

so just add the values we have for base, perpendicular and hypotenuse to these formulas now

d)
`(√(x^2+y^2) )/(y)`

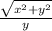
e)
`(√(x^2+y^2))/(x)`

f)
`(x)/(y)`