At what x-values do the graphs of the functions y=cos 2x and y=1-sin^2x intersect over the interval 0 < x < pi _ _

Question

asked Apr 19, 2020 101k views

2 Answers

Lumi Akimova · Answer 1 · 2020-04-26T05:59:20+0000

Answer:

No solution.

Explanation:

The given functions are

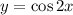$y=\cos2x$ and
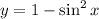$y=1-\sin^2x$ .

To find the point of intersections of the graphs of the two functions: we equate them and solve for
.

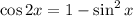
$\cos2x=1-\sin^2x$

Recall the double angle identity;
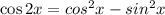
$\cos2x=cos^2x-sin^2x$

Apply this identity to obtain;

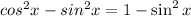
$cos^2x-sin^2x=1-\sin^2x$

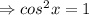
$\Rightarrow cos^2x=1$

$\cos x=\pm1$

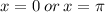
$x=0\:or\:x=\pi$

if the interval is
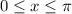$0\le x\le \pi$ , then the two graphs intersect at
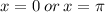
$x=0\:or\:x=\pi$

But
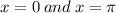$x=0\:and\:x=\pi$ does not belong to the open interval
$0\:<\:x\:<\:\pi$

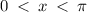
No point of intersection.