Question

After landing on an unfamiliar planet, a space explorer constructs a simple pendulum of length 55.0 cmcm. She finds that the pendulum makes 110 complete swings in a time of 145 ss.

Answer 1

Hi there!

First, let's find the period of the pendulum. This can be found by solving for the amount of time it takes for the pendulum to make ONE complete swing.

`T = \frac{\text{Total time}}{\text{Number of complete swings} }\\\\T = (145)/(110) = 1.318 s`

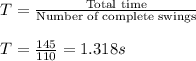
Now, let's use the equation for the period of a simple pendulum:

`T = 2\pi \sqrt{(L)/(g)}`

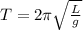
T = Period (1.318 s)
L = length of string (0.55 m)

g = acceleration due to gravity on planet (? m/s²)

Let's solve for 'g' doing some quick rearranging of the equation:

`T^2 = 4 \pi^2 ((L)/(g))\\\\g = (4\pi^2 L)/(T^2)\\\\`

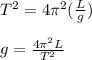
Solving for 'g' by plugging in values:

`g = (4\pi^2 (0.55))/((1.318)^2)\\ \\= \boxed{12.496 (m)/(s^2)}`