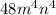Answer:
Refer to step-by-step.
Explanation:
To find the LCD of the different fractions, we first need to follow the steps of finding the LCD of algebraic fractions.
1st step: Factor
You need to factor out the expressions if they do not have a difference of two squares.
2nd step: Find the LCD of the coefficients.
You need to find the LCD of the coefficients before moving onto the variables.
3rd step: The variable part of the LCD will be every single variable you see, with the highest exponent.
So let's begin, since all the given denominators are already factored out, we can proceed straight to step 2.
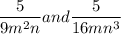
Now since we're dealing with the denominators, let's focus on them alone.
The LCD of 9 and 16 is 144
The LCD of variables m² and m is m²
The LCD of variables n and n³ is n²
So the LCD of the algebraic fractions
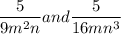 is:
is:
144m²n³
Now to the next one.
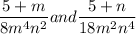
The LCD of 8 and 18 is 72
The LCD of variables
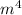 and m² is
and m² is
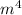
The LCD of variable n² and
 is
is

So the LCD of the algebraic fractions
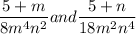 is:
is:
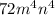
Next one we have:

The LCD of 12 and 18 is 36
The LCD of m and m³ is m³
The LCD of n and n is n
So the LCD of the algebraic fractions
 is:
is:
36m³n
Last but not the least.
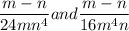
The LCD of 24 and 16 is 48
The LCD of m and
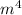 is
is
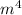
The LCD of
 and n is
and n is

So the LCD of the algebraic fractions
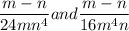 is:
is: