Question

HELP!! Type the correct answer in each box. Use numerals instead of words. If necessary, use / for the fraction bar(s).

A professor is examining a new strain of bacteria. The amount of bacteria can be modeled by function s(n) = 20 · bn, where n is the number of hours and b is an unknown positive base.
Based on the model, there were initially (answer space) bacteria.

If b = 1.85, the hourly percent growth rate of the bacteria would be
(answer space) %.

Answer 1

s(n) = 20b^n

n is the time in hours. At the beginning, the time is zero hours, so n = 0.

s(0) = 20 * b^0

s(0) = 20 * 1

s(0) = 20

The initial amount was 20.

For b = 1.85,

s(n) = 20(1.85)^n

s(n) = 20(1 + 0.85)^n

The hourly growth is 0.85.

0.85 * 100% = 85%

The hourly percent change is 85%.

Answer 2

20

85%

Explanation:

You are given the function
`S(n)=20\cdot b^n.`

If n is the number of hours, then initially n=0 and

`S(0)=20\cdot b^0=20\cdot 1=20.`

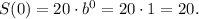
If S(n) is the function of exponential growth, then it can be represented as

`S(n)=I\cdot (1+r)^n,`

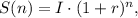
where I is the initial amount, r -is the percent growth rate and n is the number of hours.

If b = 1.85, we can represent it as b = 1 + 0.85. Thus, the hourly percent growth rate of the bacteria would be 0.85=85%.