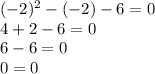Question

Factor & Finding Zeros
x^{2} -x-6=0

Answer 1

x = 3, -2

Explanation:

To help us factor, we can split the middle term up into the sum of the terms -3x and 2x:

`x^2+(-3x)+2x-6=0`

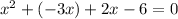
From there, we can factor out an x from the first two term and a 2 from the last two to obtain the equation

`x(x-3)+2(x-3)=0`

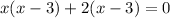
Factoring out an (x - 3) from each term gives us the equation

`(x-3)(x+2)=0`

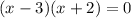
At this point, we can divide by either x - 3 or x + 2 to obtain the two equations

`x-3=0` and
`x+2=0`

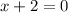
Solving both for x gives us the solutions x = 3 and x = -2. We can verify these by substituting them back into the original equation:

`3^2-3-6=0\\9-3-6=0\\6-6=0\\0=0`

`(-2)^2-(-2)-6 = 0\\4+2-6=0\\6-6=0\\0=0`