Answer: 10.52m
First, we have to establish the reference system. Let's assume that the building is on the negative y-axis and that the brick was thrown at the origin (see figure attached).
According to this, the initial velocity
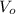 has two components, because the brick was thrown at an angle
has two components, because the brick was thrown at an angle
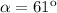 :
:
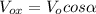 (1)
(1)
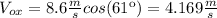 (2)
(2)
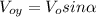 (3)
(3)
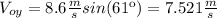 (4)
(4)
As this is a projectile motion, we have two principal equations related:
In the x-axis:
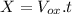 (5)
(5)
Where:
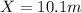 is the distance where the brick landed
is the distance where the brick landed
 is the time in seconds
is the time in seconds
If we already know
 and
and
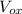 , we have to find the time (we will need it for the following equation):
, we have to find the time (we will need it for the following equation):
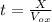 (6)
(6)
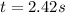 (7)
(7)
In the y-axis:
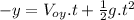 (8)
(8)
Where:
 is the height of the building (in this case it has a negative sign because of the reference system we chose)
is the height of the building (in this case it has a negative sign because of the reference system we chose)
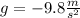 is the acceleration due gravity
is the acceleration due gravity
Substituting the known values, including the time we found on equation (7) in equation (8), we will find the height of the building:
 (9)
(9)
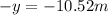 (10)
(10)
Multiplying by -1 each side of the equation:
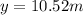 >>>>This is the height of the building
>>>>This is the height of the building