Question

Cw 10. _______thanks

Answer 1

Refer to Step-by-step

Explanation:

1. Circle P

Because the name of the circle is named by the central point of the circle.

2. Radius AP or PB

The radius is the measurement of the center of the circle to the circumference of the circle.

3. Chord DE

A chord is a line segment where both endpoints lie on the circle.

4. Diameter AB

The diameter is a line segment that goes straight across the center of a circle and the endpoints reach the circumference of the circle.

5. 12.73ft

`d = (C)/(\pi )`

`d = (40)/(\pi )`

`d=12.73ft`

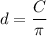
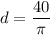
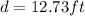
6. 4.97m

`d = (C)/(\pi )`

`d = (15.62)/(\pi )`

`d = 4.97m</p><p>`

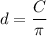
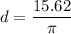
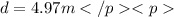
7. 132.7cm

`a^(2)+b^(2) =c^(2)`

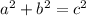
a = 5 cm

b = 12 cm

c = ?

`5^(2)+12^(2) =c^(2)`

`25+144=c^(2)`

`c^(2)=169`

`\sqrt{c^(2)}=√(169)`

`c=13cm`

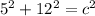
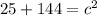
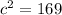
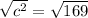
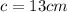
r = diameter/2

r = 13cm

r = 6.5cm

`C=\pi r^(2)`

`C=\pi 6.5^(2)`

`C=132.7cm`

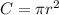
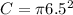
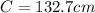
8. 128.7in

`a^(2)+b^(2) =c^(2)`

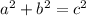
a = 9in

b = 9in

c = ?

`9^(2)+9^(2) =c^(2)`

`81+81=c^(2)`

`c^(2)=162`

`\sqrt{c^(2)}=√(162)`

`c=12.7in`

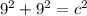
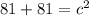
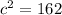
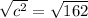
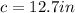
r = diameter/2

r = 12.7in/2

r = 6.4in

`C=\pi r^(2)`

`C=\pi 6.4^(2)`

`C=128.7in`

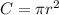
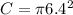
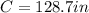
Before we proceed, let's solve for the missing arcs UT, PQ, and RQ

Arc UT = 180° - (40° + 40° + 50°)

Arc UT = 50°

Now since Arc PQ is half of the diameter, then:

Arc PQ = 90°

The same applies for Arc QR

Arc QR = 90°

9. 275°

Arc UPQ = 40°+50°+180°

Arc UPQ = 275°

10. 90°

Arc UTS = 50°+40°

Arc UTS= 90°

11. 140°

Arc RSU = 50°+40°+50°

Arc RSU = 140°

12. 270°

Arc PQS = 40°+50°+180°

Arc PQS = 270°

13. 180°

Arc PQR = 90° + 90°

Arc PQR = 180°

14. 50°

15. 130°

Arc STP = 40°+50°+40°

Arc STP = 130°

16. 320°

Arc PRU = 180° + 50° + 40° + 50°

Arc PRU = 320°