Answer:
Explanation:
(A) From the given figure, we have
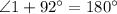 (Linear pair)
(Linear pair)
⇒
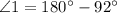
⇒
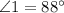
Thus, the measure of
 is
is
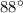 .
.
Also, using the angle sum property in the given triangle, we get
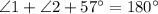
⇒
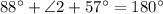
⇒
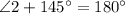
⇒
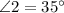
Thus, the measure of
 is
is
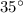 .
.
And,
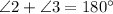
⇒
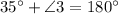
⇒

Thus, the measure of
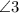 is
is
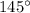 .
.
(B) Exterior angle theorem states that the exterior angle is equal to the sum of the two interior angles, thus from the given figure, we have
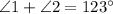
Therefore, the relationship between the measure of
 and
and
 to exterior angle is
to exterior angle is
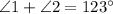 .
.