Answer:
In the figure attached we can see in a better way this situation. If we are told the rope is at 60 degress to the horizontal, we can place this rope in the origin of the X-Y coordinate system.
If we observe in detail, we have a right triangle where the opposite side
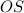 to the angle
to the angle
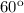 is the vertical component
is the vertical component
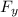 and the adjacent side
and the adjacent side
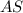 is the horizontal component
is the horizontal component
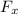 . So, we can use trigonometric functions to find the force
. So, we can use trigonometric functions to find the force
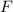 (the hypotenuse
(the hypotenuse
 ) applied to the rope.
) applied to the rope.
For
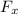 :
:
We can use the trigonometric function cosine, which is defined as:

This means
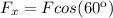
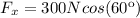
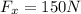
For
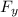 :
:
We can use the trigonometric function sine, which is defined as:
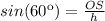
This means


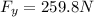
Finally the horizontal and vertical components are 150 N and 259.8 N