Question

Find the concentration of H+ ions at a pH = 11 and pH = 6. Then divide the concentration of H+ ions at a pH = 11 by the of H+ ions at a pH = 6. Record your answer in Table C. What is the concentration of H+ ions at a pH = 11? mol/L What is the concentration of H+ ions at a pH = 6? mol/L How many fewer H+ ions are there in a solution at a pH = 11 than in a solution at a pH = 6?

Answer 1

0.00000000001

0.000001

100,000

Step-by-step explanation:

Answer 2

Step-by-step explanation:

When pH of the solution is 11.

`pH=-\log[H^+]`

`11=-\log[H^+]`

`[H^+]=1* 10^(-11) M`..(1)

At pH = 11, the concentration of
`H^+` ions is
`1* 10^(-11) M`.

When the pH of the solution is 6.

`pH=-\log[H^+]'`

`6=-\log[H^+]'`

`[H^+]'=1* 10^(-6) M`..(2)

At pH = 6, the concentration of
`H^+` ions is
`1* 10^(-6) M`.

On dividing (1) by (2).

`([H^+])/([H^+]')=(1* 10^(-11) M)/(1* 10^(-6))=1* 10^(-5)`

The ratio of hydrogen ions in solution of pH equal to 11 to the solution of pH equal to 6 is
`1* 10^(-5)`.

Difference between the
`H^+` ions at both pH:

`1* 10^(-6) M-1* 10^(-11) M=9.99\time 10^(-7) M`

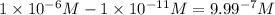
This means that Hydrogen ions in a solution at pH = 7 has
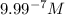`9.99\time 10^(-7) M` ions fewer than in a solution at a pH = 6