Answer:
x = 69 and y =
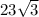
Explanation:
Firstly the hypotenuse is the side opposite the 90 degree angle. So hypotenuse is
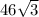
Since the angle given is 30 degree, with respect to this angle, the side length y is opposite and the side length x is adjacent.
Now, we can use trigonometric ratios to solve for x and y. Sine is defined as
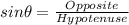 and Cos is defined as
and Cos is defined as
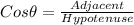
Hence, we can write:
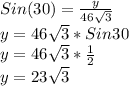
Also, we can figure out:
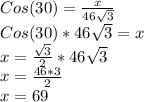
2nd answer choice is right.