Question

Need geometry help!

Answer 1

1. Area = 113.1 square units

2. Area = 28.27 square units

3. Area of Shaded = 22.27 square units

Explanation:

1.

Area of the circle is given by the formula
`A=\pi r^2`

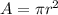
where A is the area and r is the radius

In our case the radius is 6 units, thus we have:

`A=\pi r^2\\A=\pi (6)^2\\A=\pi *36\\A=113.1`

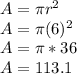
Area = 113.1 square units

2.

When we have the angle given in radians, the area of sector is given by the formula
`A=(1)/(2)r^2\theta`

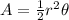
Where
`\theta` is the central angle ( in our case
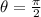`\theta = (\pi)/(2)` and r is the radius (it is 6)

Plugging in these info into the formula we have area of sector:

`A=(1)/(2)r^2\theta\\A=(1)/(2)(6)^2((\pi)/(2))\\A=(1)/(2)*36*(\pi)/(2)\\A=28.27`

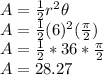
Area = 28.27 square units

3.

Area of shaded region = Area of Sector - Area of Triangle

We know area of sector is 28.27

Since the angle is 90 degrees, we have a right triangle, we can use the pythagorean theorem to find the height of the triangle, CE.

Thus

`DC^2+CE^2=DE^2\\3^2+CE^2=5^2\\9+CE^2=25\\CE^2=25-9\\CE^2=16\\CE=4`

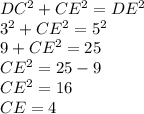
The area of triangle is
`A=(1)/(2)bh`

where b is the base (in our case it is DC = 3 ) and h is the height (in our case it is CE, which is 4). Plugging into the formula we have the area of triangle as:

`A=(1)/(2)bh\\A=(1)/(2)(3)(4)\\A=6`

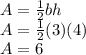
Area of Shaded = 28.27 - 6 = 22.27 square units