Question

brett has been studying a type of bacteria that doubles every month. Originally, there were 5 bacterial cells. He wants to know how many there will be after 42 months?

Answer 1

Explanation:

Originally, there were only five bacterial cells. After one month, the amount of bacteria is doubled with ten bacteria. The growth is represented by the formula:

a42 = 5 x 2^1

After 42 months, the growth can be solved using this formula:

a42 = 5 x 2^42 just so you know my cuz help me shes good in this

Answer 2

`N=2.1990232556 * 10^(13)`

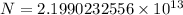
Explanation:

Given : Brett has been studying a type of bacteria that doubles every month. Originally, there were 5 bacterial cells.

To Find: He wants to know how many there will be after 42 months?

Solution:

Since we are given that initially there were 5 bacterial cells.

Bacteria doubles every month

Let n denotes the number of months .

Function becomes :
`N=N_0(2)^n`

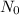`N_0` = initial amount

N = amount after n months

So,
`N=5(2)^n`

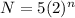
Substitute n = 42

`N=5(2)^(42)`

`N=2.1990232556 * 10^(13)`

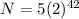
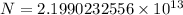
Thus there will be
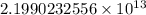`2.1990232556 * 10^(13)` bacteria after 42 months.