Question

What is the range of the cubic function f(x)=2x^3+21

A(-∞,+∞)
B(-∞,21)
C(21,+∞)
D(-∞,21)U(21,+∞)

Answer 1

Yes it’s A

Explanation:

Answer 2

A

`( - \infty , + \infty )</p><p>`

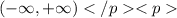
EXPLANATION.

The given function is

`f(x) = 2 {x}^(3) + 21`

Let

`y= 2 {x}^(3) + 21`

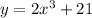
Solve for x.

`2 {x}^(3) = y - 21`

`{x}^(3) = (1)/(2) y - (21)/(2)`

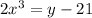
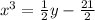
Take cubic root of both sides,

`x = \sqrt[3]{ (1)/(2) y - (21)/(2) }`

x is defined for all real values of y.

The range refers to the values of y, for which x is defined.

Hence the range is all real numbers.

In interval notation, we write this as,

`( - \infty , + \infty )</p><p>`

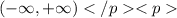
The correct choice is A.