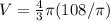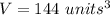Answer:
Part 1) The volume of the cylinder is
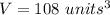
part 2) The volume of the sphere is
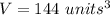
Explanation:
step 1
Find the radius of the cone
we know that
the volume of the cone is equal to
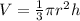
we have
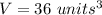
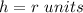
substitute and solve for r
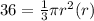
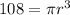
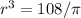 ------> equation A
------> equation A
step 2
Find the volume of the cylinder
we know that
the volume of the cylinder is equal to

we have
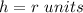
substitute
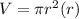
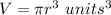
substitute the equation A in the formula above
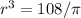 ----> equation A
----> equation A

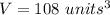
step 3
Find the volume of the sphere
we know that
The volume of the sphere is equal to
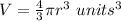
substitute the equation A in the formula above
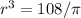 ----> equation A
----> equation A