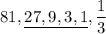Question

Insert geometric means in each geometric sequence.

( with solution )


1. ___, 24, ___, ___, 3/64



2. ___, 1/4, 1/2, ___



3. 81, ___, ___, ___, ___, 1/3


With Solution☺️!


Thank You So Much❤️✨

Answer 1

`\underline{192}, 24, \underline{3}, \underline{(3)/(8)}, (3)/(64)`

`\underline{\frac{1}8}, (1)/(4), (1)/(2), \underline{1}`

`81, \underline{27, 9, 3, 1},(1)/(3)`

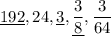
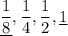
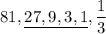
Explanation:

Given the Geometric sequences:

1. ___, 24, ___, ___, 3/64

2. ___, 1/4, 1/2, ___

3. 81, ___, ___, ___, ___, 1/3

To find:

The values in the blanks of the given geometric sequences.

Solution:

First of all, let us learn about the
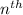`n^(th)` term of a geometric sequence.

`a_n=ar^(n-1)`

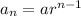
Where
`a` is the first term and

`r` is the common ratio by which each term varies from the previous term.

Considering the first sequence, we are given the second and fifth terms of the sequences.

Applying the above formula:

`ar = 24\\ar^4 = (3)/(64)`

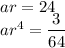
Solving the above equation:

`r = (1)/(8)`

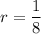
Therefore, the sequence is:

`\underline{192}, 24, \underline{3}, \underline{(3)/(8)}, (3)/(64)`

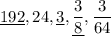
Considering the second given sequence:

`ar = (1)/(4)\\ar^2 = (1)/(2)\\\text{Solving the above equations}, r = 2`

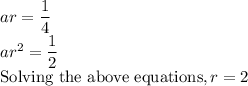
Therefore, the sequence is:

`\underline{\frac{1}8}, (1)/(4), (1)/(2), \underline{1}`

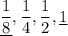
Considering the third sequence:

`a = 81\\ar^5=(1)/(3)\\\Rightarrow r = 3`

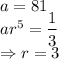
Therefore, the sequence is:

`81, \underline{27, 9, 3, 1},(1)/(3)`