Question

Which table represents a linear function​

Answer 1

Table 3 is the correct answer

Answer 2

option C

Explanation:

Given table is a linear function when the change in y to change is x is a constant.

From the tables, difference of x is a constant 1

Lets look at the difference of y values

First table

We find the change in y values

`-6+2=-4`

`-2+6=+4`

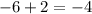
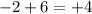
the difference is not a constant. So it is not a linear

Second table

`-5+2=3`

`-9+5= 4`

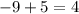
the difference is not a constant. So it is not a linear

Third table

`-10+2= -8`

`-18+10=-8`

`-26+18= -8`

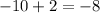
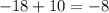
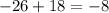
the difference is a constant. So it is a linear function.