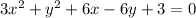2 Answers

Marco Massenzio · Answer 1 · 2020-08-27T10:54:20+0000

ANSWER

D. Ellipse;

$3{x}^(2) +{y}^(2) + 6x - 6y + 3= 0$

Step-by-step explanation

The given equation is

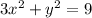
$3 {x}^(2) + {y}^(2) = 9$

Dividing through by 9 gives

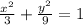
$\frac{ {x}^(2) }{ 3} + \frac{ {y}^(2) }{9} = 1$

This is the equation of an ellipse centered at the origin.

If this ellipse has been translated, so that its center is now at (-1,3), then the equation of the translated ellipse becomes

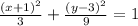
$\frac{ {(x + 1) }^(2) }{ 3} + \frac{ {(y - 3)}^(2) }{9} = 1$

We multiply through by 9 to get,

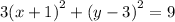
$3 {(x + 1)}^(2) + {(y - 3)}^(2) = 9$

Expand to obtain;

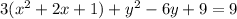
$3( {x}^(2) + 2x + 1) + {y}^(2) - 6y + 9 = 9$

Expand to obtain;

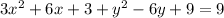
$3{x}^(2) + 6x + 3+ {y}^(2) - 6y + 9 = 9$

Regroup and equate to zero to obtain;

$3{x}^(2) +{y}^(2) + 6x - 6y + 3= 0$

Please log in or register to add a comment.