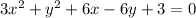ANSWER
D. Ellipse;
Step-by-step explanation
The given equation is
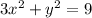
Dividing through by 9 gives
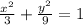
This is the equation of an ellipse centered at the origin.
If this ellipse has been translated, so that its center is now at (-1,3), then the equation of the translated ellipse becomes
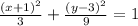
We multiply through by 9 to get,
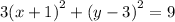
Expand to obtain;
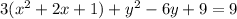
Expand to obtain;
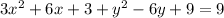
Regroup and equate to zero to obtain;