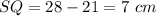Answer:
Option A.
Explanation:
we know that
In the figure
The triangles PTQ and RTS are similar by AA Similarity Theorem
so
Remember that
If two figure are similar, then the ratio of its corresponding sides is equal
so
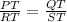
we have
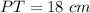
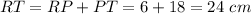
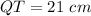
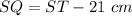 ------> equation A
------> equation A
substitute the values and solve for ST
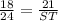
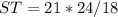
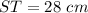
substitute the value of ST in the equation A to find the value of SQ