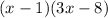Answer:
The pair of binomials are;
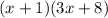
and
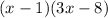
Explanation:
The given expression is
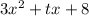
.
If the given quadratic trinomial can be factored as two binomials, then,
By comparing to
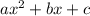
, we have
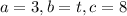
We find

We also know that;
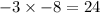
This implies that;
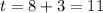
or

When t=11;
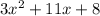
When we factor this we obtain;
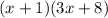
When t=-11;
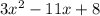
When we factor this we obtain;