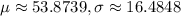Let
 be the random variable for the number of marks a given student receives on the exam.
be the random variable for the number of marks a given student receives on the exam.
10% of students obtain more than 75 marks, so
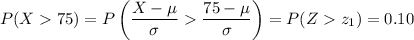
where
 follows a standard normal distribution. The critical value for an upper-tail probability of 10% is
follows a standard normal distribution. The critical value for an upper-tail probability of 10% is

where
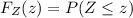 denotes the CDF of
denotes the CDF of
 , and
, and
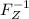 denotes the inverse CDF. We have
denotes the inverse CDF. We have
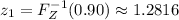
Similarly, because 20% of students obtain less than 40 marks, we have
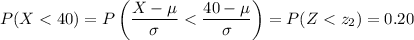
so that
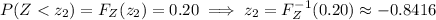
Then
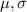 are such that
are such that


and we find