Question

A double-slit diffraction pattern is formed on a distant screen. If the separation between the slits decreases, what happens to the distance between interference fringes? Assume the angles involved remain small.

The effect cannot be determined unless the distance between the sits and the screen is known.
The distance between interference fringes increases.
The distance between interference fringes remains the same.
The distance between interference fringes also decreases.

Answer 1

The distance between interference fringes increases.

Step-by-step explanation:

In a double-slit diffraction pattern, the distance of the n-order fringe from the centre of the pattern is

`y=(n \lambda D)/(d)`

where
`\lambda` is the wavelength of the light, D the distance of the screen, and d the separation between the slits.

If we take two adjacent fringes, n and (n+1), their distance is

`\Delta y = ((n+1)\lambda D)/(d)-(n\lambda D)/(d)=(\lambda D)/(d)`

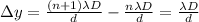
so, we see that it is inversely proportional to the slit separation, d.

Therefore, if the separation between the slits decreases, the distance between the interference fringes increases.