The terms of an arithmetic sequence are generated by adding a fixed term
 every time.
every time.
So, we start with
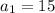 , and we continue with
, and we continue with
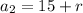 ,
,
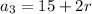 and so on.
and so on.
As you can see, the general rule is
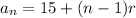
With this information, we can derive
 , knowing that
, knowing that

So, the sum of the first 100 terms is
![[tex]\displaystyle \sum_(i=0)^(99) 15+i(292)/(99) = \displaystyle \sum_(i=0)^(99) 15 + \displaystyle (292)/(99)\sum_(i=0)^(99) i = (15\cdot 99) + (292)/(99)(99\cdot 100)/(2) = 1485 + (490342)/(99)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/97gmuz0k5rddfre4l5m0s2m2jq8yqw370k.png)