Answer:
 ,
,
 , or as an ordered pair
, or as an ordered pair
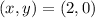 .
.
Explanation:
We have the system of equations
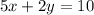 equation (1)
equation (1)
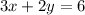 equation (2)
equation (2)
Since both equations have the term
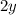 , we are using the elimination method:
, we are using the elimination method:
Step 1. Multiply equation (2) by -1 and add the result equation to equation (1):
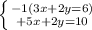
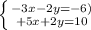
Now we can get rid of
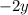
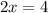
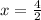

Step 2. Replace the value
 in equation (1) to find the value of
in equation (1) to find the value of
 :
:
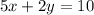
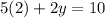
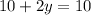
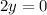
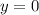
We can conclude that the solution of the system of equations is
 ,
,
 , or as an ordered pair
, or as an ordered pair
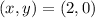 .
.