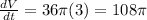Answer:
The rate of change of the volume of the cylinder when the height is 20 cm is
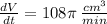
Explanation:
This is a related rates problem. In this problem, you need to find a relationship between the quantity whose rate of change you want to find, the volume in this case, and the quantity whose rates of change you know, the height of the cylinder.
We know that the volume of the cylinder is
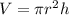
We also know that the radius is a constant, 6 cm and thus
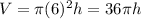
V and h both vary with time so you can differentiate both sides with respect to time, t, to get
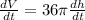
Now use the fact that
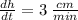 to find
to find
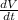 .
.