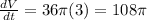Question

The height of a cylinder with a fixed radius of 6 cm is increasing at the rate of 3 cm/min. What is the rate of change of the volume of the cylinder when the height is 20cm.

Answer 1

The rate of change of the volume of the cylinder when the height is 20 cm is
`(dV)/(dt)=108\pi \:{(cm^3)/(min) }`

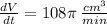
Explanation:

This is a related rates problem. In this problem, you need to find a relationship between the quantity whose rate of change you want to find, the volume in this case, and the quantity whose rates of change you know, the height of the cylinder.

We know that the volume of the cylinder is

`V=\pi r^2h`

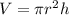
We also know that the radius is a constant, 6 cm and thus

`V=\pi (6)^2h=36\pi h`

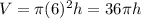
V and h both vary with time so you can differentiate both sides with respect to time, t, to get

`(dV)/(dt)=36\pi (dh)/(dt)`

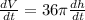
Now use the fact that
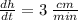`(dh)/(dt)=3 \:{(cm)/(min)` to find
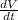`(dV)/(dt)`.

`(dV)/(dt)=36\pi (3)=108\pi`

Answer 2

108π cm^3/min

Explanation:

At a time of t min, let the height be h cm

The volume of a cylinder;

V = π r^2 h

= 36π h

differentiating both sides with respect to t;

dV/dt = 36π dh/dt

but dh/dt = 3 cm/min

dV/dt = 36π(3) = 108π cm^3/min