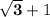Answer:
Option D.
Explanation:
The given integral is:
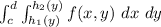
The intersection curves enclosed by the surfaces:
z = 2 - x² - y² and z = 2x + 2y
This implies that:
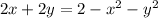
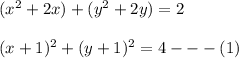
We will realize that the curve of this intersection is a circle which is centered at (-1, -1) of the radius 2.
So, from equation (1)
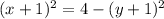
x + 1 = ±
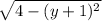
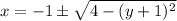
Now,
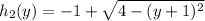 and
and
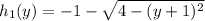
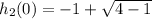
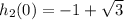 , and:
, and:
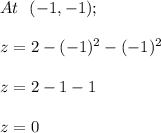
and
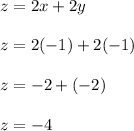
The surface z = 2-x²-y² lies above z = 2x + 2y in the region of intersection
∴
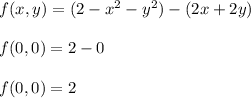
So, h₂ (0) + f(0,0) =
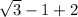
h₂ (0) + f(0,0) =